所谓“查找”记为在一个含有众多的数据元素(或记录)的查找表中找出某个“特定的”数据,即在给定信息集上寻找特定信息元素的过程。
为了便于讨论,必须给出这个“特定的”词的确切含义。首先,引入一个“关键字”的概念;关键字(Key)是数据元素(或记录)中某个数据项的值,用它可以标识(识别)一个数据元素(或记录)。
查找(Serching)根据给定的某个值,在查找表中确定一个其关键字等于给定值的记录或数据元素。若表中存在这样的一个记录,则称查找成功,此时查找的结果为给出整个记录的信息,或只是该记录在查找表中的位置;若表中不存在关键字等于给定值的记录,则称查找不成功,此时查找的结果可给出一个“空”记录或“空”指针。
查找方法有顺序查找、折半查找、分块查找、Hash表查找等。查找算法的优劣将影响到计算机的使用效率,应根据应用场合选择相应的查找算法。评价一个算法的好坏,一是时间复杂度(T(n)),n 为问题的体积,此时为表长;二是空间复杂度(D(n));三是算法的结构等其他特性;
对查找算法,主要分析其T(n)。查找过程是key的比较过程,时间主要耗费在各记录的key与给定k值的比较上,比较次数越多,算法效率越差(即T(n)量级越高),故用“比较次数”刻画算法的T(n)。另外,不能以查找某个记录的时间来作为T(n),一般以“平均查找长度”来衡量 T(n)。
9.1顺序表的查找
所谓顺序表(Sequential Table),是将表中记录(R1 、R2。。。Rn)按其序号存储于一维数组空间,其特点是相邻记录的物理位置也是相邻的。
记录Ri的类型描述如下:
typedef int data_t;
typedef struct {
data_t key; //记录key值
/* value ... */
} record_t; 顺序表类型描述如下:
#define N 1024 /* max length of list = n */
/* {R0, R1, R2, R3 ... Rn-1} are stored in from data[1] to data[n],data[0] is reserved*/
typedef struct {
record_t data[N + 1]; //顺序表空间;
int len; //当前表长,标空时len = 0;
} sqlist; 若说明: sqlist r,则(r.data[1],…….r.data[r.len])为记录表(R1、R2 …… Rn),Ri.key为r.data[i].key;
算法思路:
设给定值为k,在表(R1、R2。。。Rn)中,从Rn开始,查找key = k的记录。若存在一个记录Ri (1<i<n)的key为k,则查找成功,返回记录序号i;否则,查找失败,返回0。
算法实现:
【第一种】
int seqsearch_1(sqlist r, data_t k)
{
int i;
i = r.len;
while (i >= 1 && r.data[i].key != k)
i--;
return i;
} 我们可以看出其比较次数最大是2 * len。
【第二种】
int seqsearch_2(sqlist r, data_t k)
{
int i;
r.data[0].key = k; //k存入监视哨
i = r.len;
while (r.data[i].key != k)//顺序前往查找
i--;
return i;
} 这里比较次数最大为len。
第二种算法中引用了“监视哨”这个概念。它是放在data[0]位置的,这就我们前面讲a[0]置空的原因;监视哨在这里无需判断是否越界,这样比较次数就会少一半,这里现将k存入监视哨,若对某个i 有r.data[i].key = k,则查找成功,返回i ;若i 从n 递减到1 都无记录的key为k,i 再减1 为 0 时,必有r.data[0].key = k ,说明查找失败,返回i = 0;
对于查找算法,ASL = O(n),则效率是很低的,意味着查找某记录几乎要扫描整个表,若表长len很大时,会令人无法忍受。
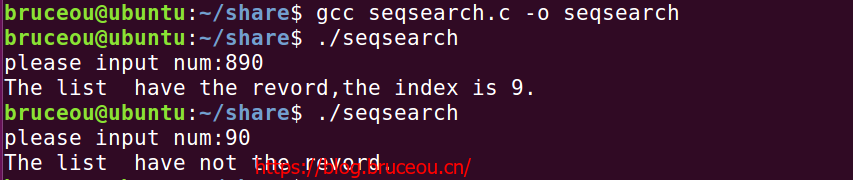
【完整代码参考1.seqsearch/seqsearch.c】
运行结果如下所示:
9.2折半查找算法
折半查找算法即二分法,二分查找算法的前提是表必须是有序的。
算法思路:
对给定值k,组不确定待查记录所在区间,每次将搜索空间减少一半(折半),知道查找成功或失败为止。
设两个指针(或游标)low 、high ,分别指向当前待查找表的上界(表头)和下界(表尾)。对于表(R1、R2。。。Rn),初始时 low = 1、high = n,令:
mid = [ (low + high) / 2 ]
指向当前待查找表中间的那个记录,下面举例说明折半查找的过程:

算法实现:
int mid_search(sqlist r,data_t k)
{
int low,high,mid;
low = 0;
high = r.len; //上下界初值
while(low <= high) //表空间存在时
{
mid = (low + high)/2; //求当前的mid
if(k == r.data[mid].key)
{
return mid; //查找成功,返回mid
}
if(k < r.data[mid].key)
{
high = mid -1; //调整上界,向左部查找
}
else
{
low = mid + 1; //调整下界,向右部查找
}
}
return 0; //low > high 查找失败
}该例子中记录表的查找过程可以用二叉树来表示:
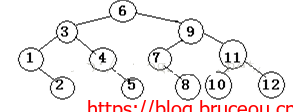
我们可以看到:找到第6个元素仅需比较一次,找到第3和第9个元素需比较2次;找到第1、4、7和10个元素许比较3次;找到第2、5、8、11个元素需比较4次;
在这个二叉树中。树中每个节点表示表中的一个记录,节点中的值为该记录在表中的位置,通常称这个描述查找过程的二叉树为判定书,从判定树上可见,查找20的过程恰好是走了一条从根到节点4的路径,和给定值进行比较的关键字个数为该路径上的节点数或节点4在判定树上的层次数。类似地,找到有序表中任意记录的过程就是走了一条从根节点到该记录相应的节点的路径,和给定值进行比较的关键字个数恰为该节点在判定树上的层次数。因此,折半查找法在查找成功时进行比较的关键字个数最多不超过树的深度,而具有n个节点的判定书的深度为[log 2 n] + 1,所以,折半查找法在查找成功时和给定值进行比较的关键字个数之多为[log2 n] + 1。n为无穷时,大大优于O(n)。
【完整代码参考2.mid_search/mid_search.c】
9.3 HASH查找
HASH表,又称散列表。在前面的讨论的顺序查找、折半查找中,其时间复杂度都在O(n)~O(log2 n)之间,不论ASL在哪个量级,都与记录长度n有关。随着n的扩大,算法的效率会越来越低。ASL 与n 有关是因为记录在存储器中的存放是随机的,或者说记录的key与记录的存放地址无关,因而查找只能建立在key的“比较”基础上。
理想的查找方法是:对给定的k,不经任何比较便能获取所需的记录,其查找的时间复杂度为常数级O(C)。这就要求在建立记录表时,确定记录的key与其存储地址之间的关系f,即使key与记录的存放地址H相对应。
9.3.1哈希查找(定义)
哈希查找是给定键值key,通过公式f (key) 直接计算数据元素的存储地址(哈希值)进行数据存储(即建立哈希表)和进行数据查找的一种方法,该公式 f 称为哈希函数。哈希查找的本质是怎么构造的表就怎么在表中查找,具有O(1)的查找效率。记为 H(key) = f (key);
不同的key 可能得到同一个Hash地址,即当 key1 != key2时,可能有 H(key1) = H(key2),此时称key1和key2为同义词。这种现象称为“冲突”或“碰撞”,因为一个单位只可存放一条记录。一般,选取Hash函数只能做到使冲突尽可能少,却不能完全避免。这就要求在出现冲突之后,寻求恰当的方法来解决冲突记录的存放问题。
9.3.2哈希查找(步骤)
建立哈希表操作步骤:
1)step1取数据元素的关键字key,计算其哈希函数值(地址)。若该地址对应的存储空间还没有被占用,则该元素存入;否则执行step2解决冲突;
2)step2根据选择的冲突处理方法,计算关键字key的下一个存储地址。若下一个存储地址仍被占用,则继续执行step2,知道找到能用的存储地址为止。
哈希查找操作步骤:
1)step1对给定key值,计算哈希地址H(key);若该地址上记录不存在,则查找失败,若记录存在且key值匹配则查找成功;否则说明发生冲突,执行step2解决冲突。
2)step2 根据选择的冲突处理方法,重复计算下一个存储地址直到找到非空记录并且key值相等才认为查找成功并结束,否则查找失败。
9.3.3哈希函数构造方法
这里主要介绍两种构造方法:1)直接地址法 2)保留除数法。

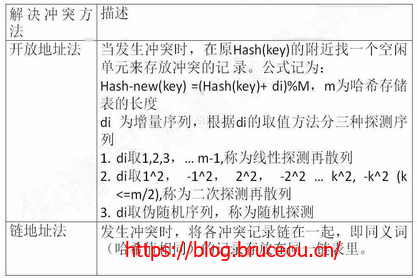
9.3.4解决冲突的方法
这里主要介绍两种解决冲突方法:1)开放地址法 2)链地址法。
9.3.5 Hash查找的使用
1、线性探查法解决冲突时Hash表的查找及插入
#define m 64 //设定表长m
typedef struct
{
keytype key; //记录关键字
.....
}Hretype;
Hretype HT[m]; //Hash表存储空间
int Lhashserch(Hretype HT[m],keytype k) //线性探查法解决冲突时的查找
{
int j,d,i = 0;
j = d = H(k); //求Hash地址并赋给j和d
while((i < m)&&(HT[j].key != NULL)&&(HT[j].key != k)
{
i ++;
j = (d + i) % m; //冲突时形成下一地址
}
if(i == m)
return -1; //表溢出时返回-1
else
return(j);
} //HT[j.key == k,查找成功;H[j].key == NULL,查找失败
void LHinsert(Hretype HT[m],Hretype R) //记录R插入Hash表的算法
{
int j = LHashserch(HT.R.key); //查找R,确定其位置
if((j == -1) || (HT[j].key == R.key)) //表溢出或记录已存
ERROR();
else
HT[j] = R; //插入HT[j]单元
} 2、链地址法解决冲突时Hash表的查找及插入
typedef struct node //记录对应节点
{
keytype key;
.....
struct node *next;
}Renode;
Renode *LinkHserch(Renode *HT[m],keytype k) //链地址法解决冲突时的查找
{
Renode *p;
int d = H(k); //求Hash地址d
p = HT[d]; //取链表头结点指针
while(p && (p->key != k))
p = p->next; //冲突时取下一同义词节点
return p;
} //查找成功时p->key == k,否则p = ^
void LHinsert(Renode HT[m],Renode *S) //将指针S所指记录插入表HT的算法
{
int d;
Renode *p;
p = LinkHserch(HT,S->key); //查找S节点
if(p)
ERROR(); //记录已存在
else
{
d =H(S->key);
S->next = HT[d];
HT[d] = S;
}
} 资源获取方法
1.关注公众号[嵌入式实验楼]
2.在公众号回复关键词[Data Structures and Algorithms]获取资料提取码

